Compartmentalized Protein-Protein Interaction Database | v2.1.1
The ComPPI scoring system is designed as a subcellular localization-based measure to score the reliablity of the interaction between two proteins. In the first step the Localization Score is calculated for all proteins that have at least one major localization. The Localization Score calculation is based on the subcellular localization evidence types for all major localizations where the given protein can be found. This approach ensures that both a) the quality of the localization (experimental, predicted, or unknown), and b) the quantity of the data (the number of sources from the integrated dataset) are considered. In the second step the previously calculated Localization Score of the interactors is used to score the interaction in a compartment-dependent manner.
In summary, the ComPPI Localization Score gives the probability of a given protein to be found in a certain major localization, while the Interaction Score is a measure for the interaction between the interactors based on the Localization Score.
Note that the Interaction Score is 0 if there were no localization data for one or both of the interactors.
We assumed that the different localization entries are independent, thus the following two basic operations have been used:
Subcellular localization data contains diverse evidence types, therefore the evidence type weights were optimized as:
The Localization Score gives the probability of a given protein to be found in a certain compartment.
A Localization Score was computed for all 6 compartments for each protein with at least one major localization using probabilistic disjunction (marked with operator V) among the different localization evidence types and the number of ComPPI localization data entries of the respective evidence type (since every entry is an additional evidence):
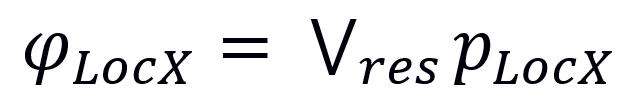(Eq. 1)
Where φLocX and pLocX are the Localization Score and the localization evidence type (experimental, unknown or predicted) for protein X and localization Loc, respectively, while res is the number of available ComPPI localization data entries for protein X.
As the first step of Interaction Score calculation, compartment-specific Interaction Scores are obtained by multiplying the Localization Scores of the two interactors for each of the 6 major compartments. Finally, the Interaction Score is calculated as the probabilistic disjunction (marked with operator V) of the Compartment-specific Interaction Scores of all major localizations available for the interacting pair from the maximal number of 6 major localizations (Eq. 2, see bottom panel of Figure 2 for details).
(Eq. 2)
Where φInt is the Interaction Score, while φLocA and φLocB are the Compartment-specific Localization Scores of interacting proteins A and B, respectively.
Localization evidence type can be experimental, unknown or predicted. Each of these is described by a parameter called the evidence type weight, and the ratio of these weights to each other has to be determined to achieve a unified scoring system applicable to the diverse data sources. We performed therefore data-driven optimization of the localization evidence type weights. Based on the fact that experimentally validated entries are the most reliable, while localization entries coming from unknown or predicted origin are less reliable, we set the following order of evidence type weights: experimental > predicted AND experimental > unknown as the two requirements of the optimization process. We chose the Human Protein Atlas (HPA) database containing only experimentally verified subcellular localizations in order to build a positive control dataset, where the interactros have at least one common localization according to HPA.
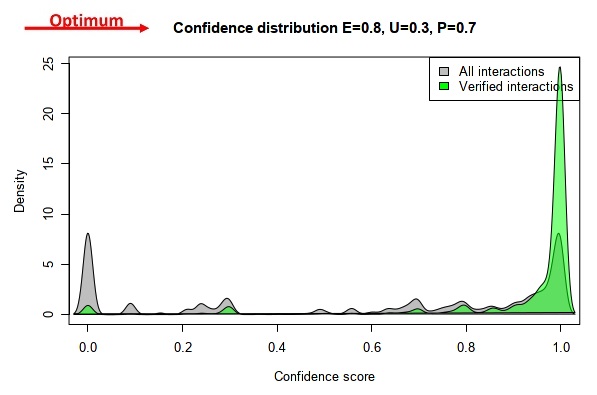
Our goal was to find a specific ratio of the experimental, unknown and predicted evidence type weight parameters that maximizes the number of high confidence interactions in the positive control dataset (HPA) and simultaneously maximizes the number of low confidence interactions in the ComPPI dataset not containing HPA data. These ensure that the quality of data marked as high confidence will match the quality of experimentally verified data. All combinations of the experimental, unknown and predicted evidence type weights were set up from 0 to 1 with 0.1 increments. The kernel density of the interactions were calculated with all these settings, which gave us the ratio of interactions belonging to a given confidence level compared to the distribution of all the interactions. Lastly, the 285 possible kernel density solutions were tested (see all possible solutions on the video below) to find the parameter combination that maximizes the number of both the low and high confidence interactions as described above.
This resulted in 0.8, 0.7, and 0.3 as the relative evidence type weights for experimental, predicted and unknown data types, respectively.
